Conic Sections/Ellipse

Definition

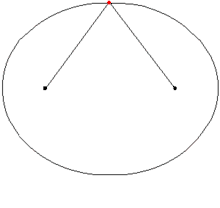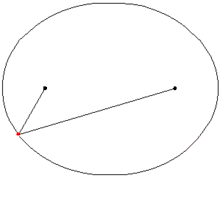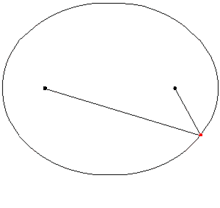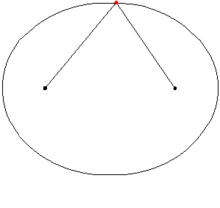
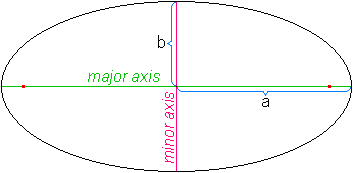
The geometric definition of an ellipse is the locus of a point which moves in a plane such that the sum of its distances from the two points called foci add up to a constant(greater than the distance between the said foci). It can also be defined as a conic where the eccentricity is less than one. Ellipses have two directrices, one on each side.

Graphing an Ellipse

The general equation for an ellipse where its major, or longer, axis is horizontal is : 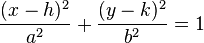$\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1$ .
Where the major axis is vertical, it is: 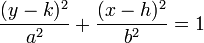$\frac{(y-k)^2}{a^2}+\frac{(x-h)^2}{b^2}=1$

The center is located at $(h,k)$ .
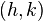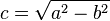The foci are found at a distance of $c$ from the centre along the major axis, where $c = \sqrt{a^2 - b^2}$ .
The eccentricity of the ellipse can be found from the formula: 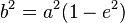$b^2 = a^2(1-e^2)$ where e is eccentricity. A higher eccentricity makes the curve appear more 'squashed', whereas an eccentricity of 0 makes the ellipse a circle.
The directrices are the lines $x = \pm ae$
The major axis has a length of 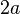$2a$ and the minor one $2b$ .
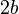The sum of the distance from each point to each of the foci is $2a$ .

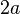Applications

Assuming a perfectly reflective perfect ellipse, any light emitted from a focus of an ellipse will be reflected to intercept the other focus. This property is exploited in "Whispering Galleries" where 2 people stand at the foci of an arbitrarily large elliptical room and can clearly hear each other whispering.
The reflective property is also useful in medicine, where it is used to treat gall stones. A machine emits sonic waves at one of the foci in an elliptical bowl, and the area of the patient where the gall stones are located is placed at the other focus. The waves are reflected and focused on the stones, causing them to be broken down and become small enough to pass from the body.
The orbit of every planet is an ellipse with the Sun at one of the two foci (Kepler's first law). The orbits of objects in space are mostly elliptical in shape.

References

http://www.purplemath.com/modules/ellipse.htm

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.