Circuit Theory/Phasors/Examples/Example 10
< Circuit Theory < Phasors < Examples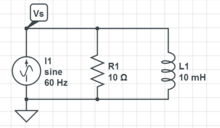
Given that the current source is defined by , find all other voltages and currents and check power.
Label Loops Junctions
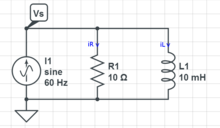
In a parallel circuit, all devices have the exact same voltage across them.
Knowns, Unknowns and Equations
- Knowns:
- Unknowns:
- Equations:
Phasor Symbolic

time domain
Evaluate the terminal relations in this order:
Substitute into this equation:
Need to formulate as a differential equation (to keep mathematicians happy) so differentiate all sides (don't let them see you doing this):
So have a differential equation that can be solved for .
Phasor domain
now transform both operations into the phasor domain ..
So:
- or
Solving for
Putting in Rectangular form:
Putting in Polar form:
back to time domain
- There will be an integration constant, but it is impossible to calculate now.
- This is from a differential equation.
- Will calculate the integration constant after adding the homogeneous solution to the above particular solution.
Phasor Numeric
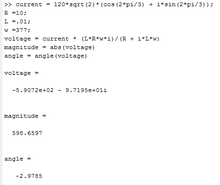
time domain
Evaluate the terminal relations in this order:
Substitute into this equation:
So have a differential equation that can be solved for :
Phasor domain

- Choosing to do calculation in time domain
back to time domain
Laplace Symbolic
time domain
Evaluate the terminal relations in this order:
Substitute into this equation:
So have a differential equation that can be solved for :
laplace domain
now transform both into the laplace domain ..
So:
Solving for
At this point the Laplace symbolic solution has to stop. The next steps depend upon the form of .
back to time domain
This can not be done without . The form of the function determines the inverse mapping.
Laplace Numeric
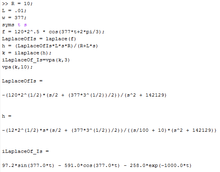
Time Domain
Laplace Domain
Time Domain
Comparison of answers
- ... from numeric solution out of phasor domain
- ... solution from substituting into symbolic time domain
Phase angles are exactly the same place in the third quadrant.
Simulation
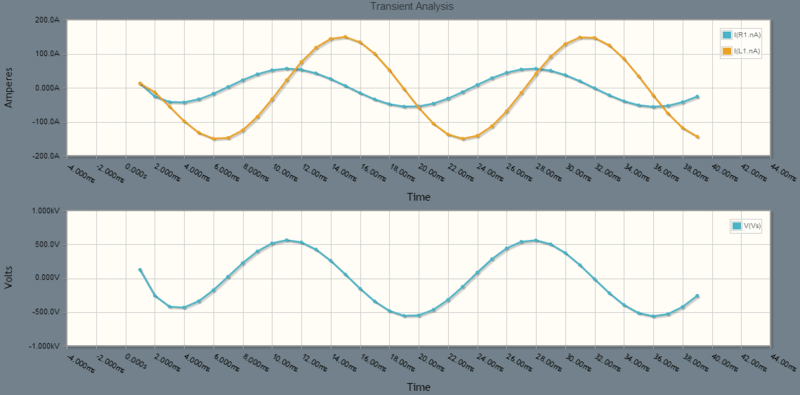
is in phase with as it should. is leading through the inductor by as it should. Everything appears centered around 0 volts, so no constants are in play.
period check
The period above looks to be between 16ms and 17ms, closer to 17ms. This agrees with the formula:
magnitude check
The magnitude of V_s is above 500 volts .. although perhaps not 600 volts.
transient response check
Everything starts out at zero. This means that only the middle to right side of the simulation windows are going to display steady state information that we can compare to calculated values.
phase check
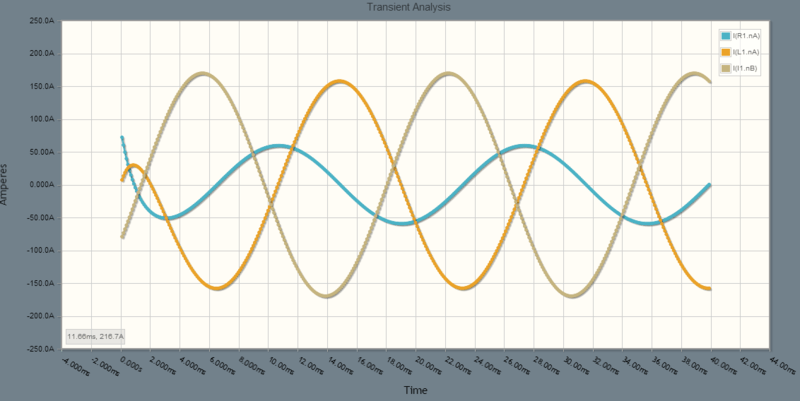
brown, blue (with same phase angle as source voltage), and (orange). (blue) leads (orange) by . The brown current (the starting point) is the starting point at 2.09 radians. The blue current should lead the brown by 3.30-2.09=1.21 radians which is 69.3 degrees which is about 3.21 ms or 1.5 squares above. This can not be seen at the beginning where the simulation software is dealing with the initial energy embalance, but by the middle of the simulation, the blue is leading the brown by about 1.5 squares. So all is well.
Power Analysis
The constants are going to add some DC power or real power to this analysis. Without knowing what they are, we can not compute their impact. So for now we stick with phasor domain power analysis:
if :, and then
and
This is a bad power factor. Power factors below .9 will cause you a visit from the utility company or the transformer on the power pole might blow. The utility's apparent power is much larger than what the customer is willing to pay.
| Value | Units | Description |
|---|---|---|
| volt-ampere va | apparent power what utility companies manage: peak power they design for, peak power they have to deliver | |
| unitless | power factor, ratio of real power to apparent power, ideally 1 | |
| watt W | real, average, active power ... what consumers want to pay for (watt-hours) | |
| volt-amp-reactive var | reactive power ... why not all outlets in a room are on the same circuit breaker |
Intuition
Should be way to do phasor math in symbol form in mupad ... probably with matrices.