Cg Programming/Unity/Projection for Virtual Reality

< Cg Programming < Unity
User in a CAVE. The user's head position is tracked and the graphics on the walls are computed for this tracked position.

This tutorial discusses off-axis perspective projection in Unity. It is based on Section “Vertex Transformations”. No shader programming is required since only the view matrix and the projection matrix are changed, which is implemented in JavaScript.

The main application of off-axis perspective projection are virtual reality environments such as the CAVE shown in the photo. Usually, the user's head position is tracked and the perspective projection for each display is computed for a camera at the tracked position such that the user experiences the illusion of looking through a window into a three-dimensional world instead of looking at a flat display.

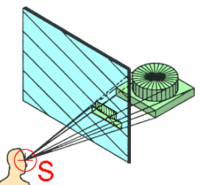
Off-axis projection is characterized by a camera position S that is not on the symmetry axis of the view plane.

Off-Axis vs. On-Axis Perspective Projection

On-axis projection refers to camera positions that are on the symmetry axis of the view plane, i.e. the axis through the center of the view plane and orthogonal to it. This case is discussed in Section “Vertex Transformations”.

In virtual reality environments, however, the virtual camera often follows the tracked position of the user's head in order to create parallax effects and thus a more compelling illusion of a three-dimensional world. Since the tracked head position is not limited to the symmetry axis of the view plane, on-axis projection is not sufficient for most virtual reality environments.

Off-axis perspective projection addresses this issue by allowing for arbitrary camera positions. While some low-level graphics APIs (e.g. older versions of OpenGL) supported off-axis projection, they had much better support for on-axis projection since this was the more common case. Similarly, many high-level tools (e.g. Unity) support off-axis projection but provide much better support for on-axis projection, i.e. you can specify any on-axis projection with some mouse clicks but you need to write a script to implement off-axis projection.

Computing Off-Axis Perspective Projection

Off-axis perspective projection requires a different view matrix and a different projection matrix than on-axis perspective projection. For the computation of the on-axis view matrix, a specified view direction is rotated onto the z axis as described in Section “Vertex Transformations”. The only difference for an off-axis view matrix is that this “view direction” is computed as the orthogonal direction to the specified view plane, i.e. the surface normal vector of the view plane.

The off-axis projection matrix has to be changed since the edges of the view plane are no longer symmetric around the intersection point with the (technical) “view direction.” Thus, the four distances to the edges have to be computed and put into a suitable projection matrix. For details, see the description by Robert Kooima in his publication “Generalized Perspective Projection”. The next section presents an implementation of this technique in Unity.

Camera Script

The following script is based on the code in Robert Kooima's publication. There are very few implementation differences. One is that, in Unity, the view plane is more easily specified as a built-in Plane object, which has corners at (±5, 0, ±5) in object coordinates. Furthermore, the original code was written for a right-handed coordinate system while Unity uses a left-handed coordinate system; thus, the result of all cross products has to be multiplied with -1. Also, the code here takes into account that the camera might be seeing the back-face of the Plane object.

Another difference is that the rotation of the camera's GameObject and the parameter fieldOfView are used by Unity for view frustum culling; therefore, the script should set those values to appropriate values. (These values have no meaning for the computation of the matrices.) Unfortunately, this might cause problems if other scripts (namely the script that sets the tracked head position) are also setting the camera rotation. Therefore, this estimation can be deactivated with the variable estimateViewFrustum (at the risk of incorrect view frustum culling by Unity).

If the parameter setNearClipPlane is set to true, the script sets the distance of the near clip plane to the distance between the camera and the view plane plus the value of nearClipDistanceOffset. This functionality is particularly useful when using the script to render mirrors as described in Section “Mirrors”. nearClipDistanceOffset should then be a negative number that is as close to 0 as possible while avoiding artifacts.

// This script should be attached to a Camera object 
// in Unity. Once a Plane object is specified as the 
// "projectionScreen", the script computes a suitable
// view and projection matrix for the camera.
// The code is based on Robert Kooima's publication  
// "Generalized Perspective Projection," 2009, 
// http://csc.lsu.edu/~kooima/pdfs/gen-perspective.pdf 

// Use the following line to apply the script in the editor:
// @script ExecuteInEditMode()

#pragma strict


public var projectionScreen : GameObject;
public var estimateViewFrustum : boolean = true;
public var setNearClipPlane : boolean = false;
public var nearClipDistanceOffset : float = -0.01;

private var cameraComponent : Camera;

function LateUpdate() {
   cameraComponent = GetComponent(Camera);
   if (null != projectionScreen && null != cameraComponent)
   {
      var pa : Vector3 =  
         projectionScreen.transform.TransformPoint(
         Vector3(-5.0, 0.0, -5.0));
         // lower left corner in world coordinates
      var pb : Vector3 = 
         projectionScreen.transform.TransformPoint(
         Vector3(5.0, 0.0, -5.0));
         // lower right corner
      var pc : Vector3 = 
         projectionScreen.transform.TransformPoint(
         Vector3(-5.0, 0.0, 5.0));
         // upper left corner
      var pe : Vector3 = transform.position;
         // eye position
      var n : float = cameraComponent.nearClipPlane;
         // distance of near clipping plane
      var f : float = cameraComponent.farClipPlane;
         // distance of far clipping plane

      var va : Vector3; // from pe to pa
      var vb : Vector3; // from pe to pb
      var vc : Vector3; // from pe to pc
      var vr : Vector3; // right axis of screen
      var vu : Vector3; // up axis of screen
      var vn : Vector3; // normal vector of screen
		
      var l : float; // distance to left screen edge
      var r : float; // distance to right screen edge
      var b : float; // distance to bottom screen edge
      var t : float; // distance to top screen edge
      var d : float; // distance from eye to screen 

      vr = pb - pa;
      vu = pc - pa;
      va = pa - pe;
      vb = pb - pe;
      vc = pc - pe;

      // are we looking at the backface of the plane object?
      if (Vector3.Dot(-Vector3.Cross(va, vc), vb) < 0.0)
      {
         // mirror points along the z axis (most users 
         // probably expect the x axis to stay fixed)
         vu = -vu;
         pa = pc;
         pb = pa + vr;
         pc = pa + vu;
         va = pa - pe;
         vb = pb - pe;
         vc = pc - pe;
      }

      vr.Normalize();
      vu.Normalize();
      vn = -Vector3.Cross(vr, vu); 
         // we need the minus sign because Unity 
         // uses a left-handed coordinate system
      vn.Normalize();
			
      d = -Vector3.Dot(va, vn);
      if (setNearClipPlane)
      {
         n = d + nearClipDistanceOffset;
         cameraComponent.nearClipPlane = n;
      }
      l = Vector3.Dot(vr, va) * n / d;
      r = Vector3.Dot(vr, vb) * n / d;
      b = Vector3.Dot(vu, va) * n / d;
      t = Vector3.Dot(vu, vc) * n / d;

      var p : Matrix4x4; // projection matrix 
      p[0,0] = 2.0*n/(r-l); 
      p[0,1] = 0.0; 
      p[0,2] = (r+l)/(r-l); 
      p[0,3] = 0.0;

      p[1,0] = 0.0; 
      p[1,1] = 2.0*n/(t-b); 
      p[1,2] = (t+b)/(t-b); 
      p[1,3] = 0.0;

      p[2,0] = 0.0;         
      p[2,1] = 0.0; 
      p[2,2] = (f+n)/(n-f); 
      p[2,3] = 2.0*f*n/(n-f);

      p[3,0] = 0.0;         
      p[3,1] = 0.0; 
      p[3,2] = -1.0;        
      p[3,3] = 0.0;		

      var rm : Matrix4x4; // rotation matrix;
      rm[0,0] = vr.x; 
      rm[0,1] = vr.y; 
      rm[0,2] = vr.z; 
      rm[0,3] = 0.0;	
	
      rm[1,0] = vu.x; 
      rm[1,1] = vu.y; 
      rm[1,2] = vu.z; 
      rm[1,3] = 0.0;	
	
      rm[2,0] = vn.x; 
      rm[2,1] = vn.y; 
      rm[2,2] = vn.z; 
      rm[2,3] = 0.0;	
	
      rm[3,0] = 0.0;  
      rm[3,1] = 0.0;  
      rm[3,2] = 0.0;  
      rm[3,3] = 1.0;		

      var tm : Matrix4x4; // translation matrix;
      tm[0,0] = 1.0; 
      tm[0,1] = 0.0; 
      tm[0,2] = 0.0; 
      tm[0,3] = -pe.x;	
	
      tm[1,0] = 0.0; 
      tm[1,1] = 1.0; 
      tm[1,2] = 0.0; 
      tm[1,3] = -pe.y;	
	
      tm[2,0] = 0.0; 
      tm[2,1] = 0.0; 
      tm[2,2] = 1.0; 
      tm[2,3] = -pe.z;	
	
      tm[3,0] = 0.0; 
      tm[3,1] = 0.0; 
      tm[3,2] = 0.0; 
      tm[3,3] = 1.0;		

      // set matrices
      cameraComponent.projectionMatrix = p;
      cameraComponent.worldToCameraMatrix = rm * tm; 
      // The original paper puts everything into the projection 
      // matrix (i.e. sets it to p * rm * tm and the other 
      // matrix to the identity), but this doesn't appear to 
      // work with Unity's shadow maps.

      if (estimateViewFrustum)
      {
         // rotate camera to screen for culling to work
         var q : Quaternion;
         q.SetLookRotation((0.5 * (pb + pc) - pe), vu); 
             // look at center of screen
         cameraComponent.transform.rotation = q;

         // set fieldOfView to a conservative estimate 
         // to make frustum tall enough
         if (cameraComponent.aspect >= 1.0)
         { 
            cameraComponent.fieldOfView = Mathf.Rad2Deg * 
               Mathf.Atan(((pb-pa).magnitude + (pc-pa).magnitude) 
               / va.magnitude);
         }
         else 
         {
             // take the camera aspect into account to 
             // make the frustum wide enough 
             cameraComponent.fieldOfView = 
                Mathf.Rad2Deg / cameraComponent.aspect *
                Mathf.Atan(((pb-pa).magnitude + (pc-pa).magnitude) 
                / va.magnitude);
         }	
      }
   }
}

To use this script, choose Create > Javascript in the Project Window, double-click the new script to edit it, and copy & paste the code from above into it. Then attach the script to your main camera (drag it from the Project Window over the camera object in the Hierarchy Window). Furthermore, create a Plane object (GameObject > 3D Object > Plane in the main menu) and place it into the virtual scene to define the view plane. Deactivate the Mesh Renderer of the Plane in the Inspector Window to make it invisible (it is only a placeholder). Select the camera object and drag the plane object to Projection Screen in the Inspector. The script will be active when the game is started. Add the line

@script ExecuteInEditMode()

at the top of the code to make the script also run in the editor.

Note that there are probably some parts of Unity that ignore the new projection matrix and that therefore are unusable in combination with this script.

Summary

In this tutorial, we have looked at:

Further Reading

If you want to know more


< Cg Programming/Unity

Unless stated otherwise, all example source code on this page is granted to the public domain.
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.