Calculus/Lines and Planes in Space

Introduction

For many practical applications, for example for describing forces in physics and mechanics, you have to work with the mathematical descriptions of lines and planes in 3-dimensional space.

Parametric Equations

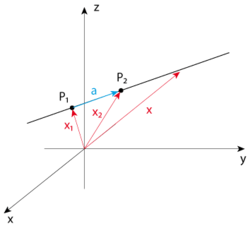
Line in Space

A line in space is defined by two points in space, which I will call $P_{1}$ and $P_{2}$ . Let ${\mathbf {x}}_{1}$ be the vector from the origin to $P_{1}$ , and ${\mathbf {x}}_{2}$ the vector from the origin to $P_{2}$ . Given these two points, every other point $P$ on the line can be reached by

{\mathbf {x}}={\mathbf {x}}_{1}+\lambda {\mathbf {a}}

where ${\mathbf {a}}$ is the vector from $P_{1}$ and $P_{2}$ :

{\mathbf {a}}={\mathbf {x}}_{2}-{\mathbf {x}}_{1}

Plane in Space

The same idea can be used to describe a plane in 3-dimensional space, which is uniquely defined by three points (which do not lie on a line) in space ( $P_{1},P_{2},P_{3}$ ). Let ${\mathbf {x}}_{i}$ be the vectors from the origin to $P_{i}$ . Then

{\mathbf {x}}={\mathbf {x}}_{1}+\lambda {\mathbf {a}}+\mu {\mathbf {b}}

with:

{\mathbf {a}}={\mathbf {x}}_{2}-{\mathbf {x}}_{1}\,\,{\text{and}}\,\,{\mathbf {b}}={\mathbf {x}}_{3}-{\mathbf {x}}_{1}

Note that the starting point does not have to be ${\mathbf {x}}_{1}$ , but can be any point in the plane. Similarly, the only requirement on the vectors ${\mathbf {a}}$ and ${\mathbf {b}}$ is that they have to be two non-collinear vectors in our plane.

Vector Equation (of a Plane in Space, or of a Line in a Plane)

An alternative representation of a Plane in Space is obtained by observing that a plane is defined by a point $P_{1}$ in that plane and a direction perpendicular to the plane, which we denote with the vector ${\mathbf {n}}$ . As above, let ${\mathbf {x}}_{1}$ describe the vector from the origin to $P_{1}$ , and ${\mathbf {x}}$ the vector from the origin to another point $P$ in the plane. Since any vector that lies in the plane is perpendicular to ${\mathbf {n}}$ , the vector equation of the plane is given by

{\mathbf {n}}\cdot ({\mathbf {x}}-{\mathbf {x}}_{1})=0

In 2 dimensions, the same equation uniquely describes a Line.

Scalar Equation (of a Plane in Space, or of a Line in a Plane)

If we express ${\mathbf {n}}$ and ${\mathbf {x}}$ through their components

{\mathbf {n}}=\left({{\begin{array}{*{20}c}a\\b\\c\\\end{array}}}\right),\,\,{\text{and}}\,\,{\mathbf {x}}=\left({{\begin{array}{*{20}c}x\\y\\z\\\end{array}}}\right),

writing out the scalar product for ${\mathbf {n}}\cdot ({\mathbf {x}}-{\mathbf {x}}_{1})=0$ provides us with the scalar equation for a plane in space:

ax+by+cz=d

where $d={\mathbf {n}}\cdot {\mathbf {x}}_{1}$ .

In 2d space, the equivalent steps lead to the scalar equation for a line in a plane:

ax+by=c

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.