Calculus/Differentiation/Applications of Derivatives/Exercises

< Calculus < Differentiation < Applications of Derivatives

Relative Extrema

Find the relative maximum(s) and minimum(s), if any, of the following functions.

f(x)={\frac {x}{x+1}}

f(x)={\sqrt[{3}]{(x-1)^{2}}}

f(x)=x^{2}+{\frac {2}{x}}

f(s)={\frac {s}{1+s^{2}}}

f(x)=x^{2}-4x+9

f(x)={\frac {x^{2}+x+1}{x^{2}-x+1}}

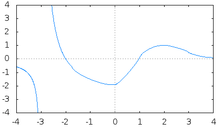
Range of Function

7. Show that the expression

x+{\frac {1}{x}}

cannot take on any value strictly between 2 and -2.

Since $f''(-1)$ is negative, $x=-1$ corresponds to a relative maximum.
${\begin{aligned}&f(-1)=-2\\&\lim \limits _{x\to -\infty }f(x)=-\infty \end{aligned}}$

For $x<-1$ , $f'(x)$ is positive, which means that the function is increasing. Coming from very negative $x$ -values, $f$ increases from a very negative value to reach a relative maximum of $-2$ at $x=-1$ .
For $-1<x<1$ , $f'(x)$ is negative, which means that the function is decreasing.
$\lim _{x\to 0^{-}}f(x)=-\infty$
$\lim _{x\to 0^{+}}f(x)=\infty$
$f''(1)=2$
Since $f''(1)$ is positive, $x=1$ corresponds to a relative minimum.
$f(1)=2$
Between $[-1,0)$ the function decreases from $-2$ to $-\infty$ , then jumps to $+\infty$ and decreases until it reaches a relative minimum of $2$ at $x=1$ .
For $x>1$ , $f'(x)$ is positive, so the function increases from a minimum of $2$ .
The above analysis shows that there is a gap in the function's range between $-2$ and $2$ .

Absolute Extrema

Determine the absolute maximum and minimum of the following functions on the given domain

f(x)={\frac {x^{3}}{3}}-{\frac {x^{2}}{2}}+1

[0,3]

f(x)=\left({\frac {4}{3}}x^{2}-1\right)x

[-{\tfrac {1}{2}},2]

Determine Intervals of Change

Find the intervals where the following functions are increasing or decreasing

10.

f(x)=10-6x-2x^{2}

11.

f(x)=2x^{3}-12x^{2}+18x+15

12.

f(x)=5+36x+3x^{2}-2x^{3}

13.

f(x)=8+36x+3x^{2}-2x^{3}

14.

f(x)=5x^{3}-15x^{2}-120x+3

15.

f(x)=x^{3}-6x^{2}-36x+2

Determine Intervals of Concavity

Find the intervals where the following functions are concave up or concave down

16.

f(x)=10-6x-2x^{2}

17.

f(x)=2x^{3}-12x^{2}+18x+15

18.

f(x)=5+36x+3x^{2}-2x^{3}

19.

f(x)=8+36x+3x^{2}-2x^{3}

20.

f(x)=5x^{3}-15x^{2}-120x+3

21.

f(x)=x^{3}-6x^{2}-36x+2

Word Problems

22. You peer around a corner. A velociraptor 64 meters away spots you. You run away at a speed of 6 meters per second. The raptor chases, running towards the corner you just left at a speed of

4t

meters per second (time

t

measured in seconds after spotting). After you have run 4 seconds the raptor is 32 meters from the corner. At this time, how fast is death approaching your soon to be mangled flesh? That is, what is the rate of change in the distance between you and the raptor?

23. Two bicycles leave an intersection at the same time. One heads north going

12{\rm {mph}}

and the other heads east going

5{\rm {mph}}

. How fast are the bikes getting away from each other after one hour?

24. You're making a can of volume

200m^{3}

with a gold side and silver top/bottom. Say gold costs 10 dollars per m

^{2}

and silver costs 1 dollar per

m^{2}

. What's the minimum cost of such a can?

Graphing Functions

For each of the following, graph a function that abides by the provided characteristics

25.

f(1)=f(-2)=0,\ \lim _{x\to \infty }f(x)=\lim _{x\to -\infty }f(x)=0,\ {\mbox{ vertical asymptote at }}x=-3,\ f'(x)>0{\mbox{ on }}(0,2),

f'(x)<0{\mbox{ on }}(-\infty ,-3)\cup (-3,0)\cup (2,\infty ),\ f''(x)>0{\mbox{ on }}(-3,1)\cup (3,\infty ),\ f''(x)<0{\mbox{ on }}(-\infty ,-3)\cup (1,3).

26.

f{\mbox{ has domain }}[-1,1],\ f(-1)=-1,\ f(-{\tfrac {1}{2}})=-2,\ f'(-{\tfrac {1}{2}})=0,\ f''(x)>0{\mbox{ on }}(-1,1)

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.