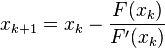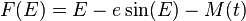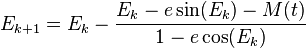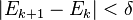Astrodynamics/The Kepler Problem

< Astrodynamics
Astrodynamics

The Kepler Problem

While Kepler's equation is easy to solve for time, there is no general solution for the reverse problem. To determine eccentric anomaly (and thus spacecraft position) at a given time, generally an iterative numerical method is used, such as Newton's method:

x_{k+1}=x_{k}-\frac{F(x_k)}{F'(x_k)}

Where

F(E) = E - e \sin(E) - M(t)

The iteration takes the form

E_{k+1}=E_{k} - \frac{ E_{k} - e \sin(E_{k}) - M(t) }{ 1 - e \cos(E_{k})}

For most elliptical orbits an initial guess of E0 = M is sufficient; for orbits with eccentricities greater than 0.8, E0 = π may be used. Better initial guesses are possible, but are not generally required. The iterative process is repeated until required accuracy conditions are achieved, for example:

|E_{k+1}-E_k|<\delta

Where δ is the desired accuracy.

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.