Ada Programming/Type System

Ada's type system allows the programmer to construct powerful abstractions that represent the real world, and to provide valuable information to the compiler, so that the compiler can find many logic or design errors before they become bugs. It is at the heart of the language, and good Ada programmers learn to use it to great advantage. Four principles govern the type system:

• Strong typing: types are incompatible with one another, so it is not possible to mix apples and oranges. There are, however, ways to convert between types.
• Static typing: type checked while compiling, this allows type errors to be found earlier.
• Abstraction: types represent the real world or the problem at hand; not how the computer represents the data internally. There are ways to specify exactly how a type must be represented at the bit level, but we will defer that discussion to another chapter.
• Name equivalence, as opposed to structural equivalence used in most other languages. Two types are compatible if and only if they have the same name; not if they just happen to have the same size or bit representation. You can thus declare two integer types with the same ranges that are totally incompatible, or two record types with exactly the same components, but which are incompatible.

Types are incompatible with one another. However, each type can have any number of subtypes, which are compatible with their base type and may be compatible with one another. See below for examples of subtypes which are incompatible with one another.

Predefined types

There are several predefined types, but most programmers prefer to define their own, application-specific types. Nevertheless, these predefined types are very useful as interfaces between libraries developed independently. The predefined library, obviously, uses these types too.

These types are predefined in the Standard package:

Integer

This type covers at least the range .. (RM 3.5.4 (21) (Annotated)). The Standard also defines Natural and Positive subtypes of this type.

Float

There is only a very weak implementation requirement on this type (RM 3.5.7 (14) (Annotated)); most of the time you would define your own floating-point types, and specify your precision and range requirements.

Duration

A fixed point type used for timing. It represents a period of time in seconds (RM A.1 (43) (Annotated)).

Character 

A special form of Enumerations. There are three predefined kinds of character types: 8-bit characters (called Character), 16-bit characters (called Wide_Character), and 32-bit characters (Wide_Wide_Character). Character has been present since the first version of the language (Ada 83), Wide_Character was added in Ada 95, while the type Wide_Wide_Character is available with Ada 2005.

String

Three indefinite array types, of Character, Wide_Character, and Wide_Wide_Character respectively. The standard library contains packages for handling strings in three variants: fixed length (Ada.Strings.Fixed), with varying length below a certain upper bound (Ada.Strings.Bounded), and unbounded length (Ada.Strings.Unbounded). Each of these packages has a Wide_ and a Wide_Wide_ variant.

Boolean 

A Boolean in Ada is an Enumeration of False and True with special semantics.

Packages System and System.Storage_Elements predefine some types which are primarily useful for low-level programming and interfacing to hardware.

System.Address 

An address in memory.

System.Storage_Elements.Storage_Offset 

An offset, which can be added to an address to obtain a new address. You can also subtract one address from another to get the offset between them. Together, Address, Storage_Offset and their associated subprograms provide for address arithmetic.

System.Storage_Elements.Storage_Count 

A subtype of Storage_Offset which cannot be negative, and represents the memory size of a data structure (similar to C's size_t).

System.Storage_Elements.Storage_Element 

In most computers, this is a byte. Formally, it is the smallest unit of memory that has an address.

System.Storage_Elements.Storage_Array 

An array of Storage_Elements without any meaning, useful when doing raw memory access.

The Type Hierarchy

Types are organized hierarchically. A type inherits properties from types above it in the hierarchy. For example, all scalar types (integer, enumeration, modular, fixed-point and floating-point types) have operators "<", ">" and arithmetic operators defined for them, and all discrete types can serve as array indexes.

Ada type hierarchy

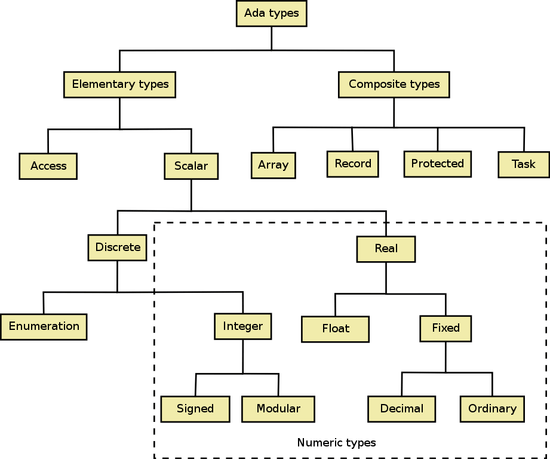
Here is a broad overview of each category of types; please follow the links for detailed explanations. Inside parenthesis there are equivalences in C and Pascal for readers familiar with those languages.

Signed Integers (int, INTEGER) 

Signed Integers are defined via the range of values needed.

Unsigned Integers (unsigned, CARDINAL) 

Unsigned Integers are called Modular Types. Apart from being unsigned they also have wrap-around functionality.

Enumerations (enum, char, bool, BOOLEAN) 

Ada Enumeration types are a separate type family.

Floating point (float, double, REAL) 

Floating point types are defined by the digits needed, the relative error bound.

Ordinary and Decimal Fixed Point (DECIMAL) 

Fixed point types are defined by their delta, the absolute error bound.

Arrays ( [ ], ARRAY [ ] OF, STRING ) 

Arrays with both compile-time and run-time determined size are supported.

Record (struct, class, RECORD OF) 

A record is a composite type that groups one or more fields.

Access (*, ^, POINTER TO) 

Ada's Access types may be more than just a simple memory address.

Task & Protected (no equivalence in C or Pascal) 

Task and Protected types allow the control of concurrency

Interfaces (no equivalence in C or Pascal) 

New in Ada 2005, these types are similar to the Java interfaces.

Classification of Types

The types of this hierarchy can be classified as follows.

Specific vs. Class-wide

type T is ...  -- specific
  T'Class      -- class-wide

Operations of specific types are non-dispatching, those on class-wide types are dispatching.

New types can be declared by deriving from specific types; primitive operations are inherited by derivation. You cannot derive from class-wide types.

Constrained vs. Unconstrained

type I is range 1 .. 10;           -- constrained
type AC is array (1 .. 10) of ...  -- constrained

type AU is array (I range <>) of ...          -- unconstrained
type R (X: Discriminant [:= Default]) is ...  -- unconstrained

By giving a constraint to an unconstrained subtype, a subtype or object becomes constrained:

subtype RC is R (Value);  -- constrained subtype of R
OC: R (Value);            -- constrained object of anonymous constrained subtype of R
OU: R;                    -- unconstrained object

Declaring an unconstrained object is only possible if a default value is given in the type declaration above. The language does not specify how such objects are allocated. GNAT allocates the maximum size, so that size changes that might occur with discriminant changes present no problem. Another possibility is implicit dynamic allocation on the heap and re-allocation followed by a deallocation when the size changes.

Definite vs. Indefinite

type I is range 1 .. 10;                     -- definite
type RD (X: Discriminant := Default) is ...  -- definite

type T (<>) is ...                    -- indefinite
type AU is array (I range <>) of ...  -- indefinite
type RI (X: Discriminant) is ...      -- indefinite

Definite subtypes allow the declaration of objects without initial value, since objects of definite subtypes have constraints that are known at creation-time. Object declarations of indefinite subtypes need an initial value to supply a constraint; they are then constrained by the constraint delivered by the initial value.

OT: T  := Expr;                       -- some initial expression (object, function call, etc.)
OA: AU := (3 => 10, 5 => 2, 4 => 4);  -- index range is now 3 .. 5
OR: RI := Expr;                       -- again some initial expression as above

Unconstrained vs. Indefinite

Note that unconstrained subtypes are not necessarily indefinite as can be seen above with RD: it is a definite unconstrained subtype.

Concurrency Types

The Ada language uses types for one more purpose in addition to classifying data + operations. The type system integrates concurrency (threading, parallelism). Programmers will use types for expressing the concurrent threads of control of their programs.

The core pieces of this part of the type system, the task types and the protected types are explained in greater depth in a section on tasking.

Limited Types

Limiting a type means disallowing assignment. The “concurrency types” described above are always limited. Programmers can define their own types to be limited, too, like this:

type T is limited …;

(The ellipsis stands for private, or for a record definition, see the corresponding subsection on this page.) A limited type also doesn't have an equality operator unless the programmer defines one.

You can learn more in the limited types chapter.

Defining new types and subtypes

You can define a new type with the following syntax:

type T is...

followed by the description of the type, as explained in detail in each category of type.

Formally, the above declaration creates a type and its first subtype named T. The type itself, correctly called the "type of T", is anonymous; the RM refers to it as T (in italics), but often speaks sloppily about the type T. But this is an academic consideration; for most purposes, it is sufficient to think of T as a type. For scalar types, there is also a base type called T'Base, which encompasses all values of T.

For signed integer types, the type of T comprises the (complete) set of mathematical integers. The base type is a certain hardware type, symmetric around zero (except for possibly one extra negative value), encompassing all values of T.

As explained above, all types are incompatible; thus:

type Integer_1 is range 1 .. 10;
type Integer_2 is range 1 .. 10;
A : Integer_1 := 8;
B : Integer_2 := A; -- illegal!

is illegal, because Integer_1 and Integer_2 are different and incompatible types. It is this feature which allows the compiler to detect logic errors at compile time, such as adding a file descriptor to a number of bytes, or a length to a weight. The fact that the two types have the same range does not make them compatible: this is name equivalence in action, as opposed to structural equivalence. (Below, we will see how you can convert between incompatible types; there are strict rules for this.)

Creating subtypes

You can also create new subtypes of a given type, which will be compatible with each other, like this:

type Integer_1 is range 1 .. 10;
subtype Integer_2 is Integer_1      range 7 .. 11;  -- bad
subtype Integer_3 is Integer_1'Base range 7 .. 11;  -- OK
A : Integer_1 := 8;
B : Integer_3 := A; -- OK

The declaration of Integer_2 is bad because the constraint 7 .. 11 is not compatible with Integer_1; it raises Constraint_Error at subtype elaboration time.

Integer_1 and Integer_3 are compatible because they are both subtypes of the same type, namely Integer_1'Base.

It is not necessary that the subtype ranges overlap, or be included in one another. The compiler inserts a run-time range check when you assign A to B; if the value of A, at that point, happens to be outside the range of Integer_3, the program raises Constraint_Error.

There are a few predefined subtypes which are very useful:

subtype Natural  is Integer range 0 .. Integer'Last;
subtype Positive is Integer range 1 .. Integer'Last;

Derived types

A derived type is a new, full-blown type created from an existing one. Like any other type, it is incompatible with its parent; however, it inherits the primitive operations defined for the parent type.

type Integer_1 is range 1 .. 10;
type Integer_2 is new Integer_1 range 2 .. 8;
A : Integer_1 := 8;
B : Integer_2 := A; -- illegal!

Here both types are discrete; it is mandatory that the range of the derived type be included in the range of its parent. Contrast this with subtypes. The reason is that the derived type inherits the primitive operations defined for its parent, and these operations assume the range of the parent type. Here is an illustration of this feature:

procedure Derived_Types is

   package Pak is
      type Integer_1 is range 1 .. 10;
      procedure P (I: in Integer_1); -- primitive operation, assumes 1 .. 10
      type Integer_2 is new Integer_1 range 8 .. 10; -- must not break P's assumption
      -- procedure P (I: in Integer_2);  inherited P implicitly defined here
   end Pak;

   package body Pak is
      -- omitted
   end Pak;

   use Pak;
   A: Integer_1 := 4;
   B: Integer_2 := 9;

begin

   P (B); -- OK, call the inherited operation

end Derived_Types;

When we call P (B), the parameter B is converted to Integer_1; this conversion of course passes since the set of acceptable values for the derived type (here, 8 .. 10) must be included in that of the parent type (1 .. 10). Then P is called with the converted parameter.

Consider however a variant of the example above:

procedure Derived_Types is

  package Pak is
    type Integer_1 is range 1 .. 10;
    procedure P (I: in Integer_1; J: out Integer_1);
    type Integer_2 is new Integer_1 range 8 .. 10;
  end Pak;

  package body Pak is
    procedure P (I: in Integer_1; J: out Integer_1) is
    begin
      J := I - 1;
    end P;
  end Pak;

  use Pak;

  A: Integer_1 := 4;  X: Integer_1;
  B: Integer_2 := 8;  Y: Integer_2;

begin

  P (A, X);
  P (B, Y);

end Derived_Types;

When P (B, Y) is called, both parameters are converted to Integer_1. Thus the range check on J (7) in the body of P will pass. However on return parameter Y is converted back to Integer_2 and the range check on Y will of course fail.

With the above in mind, you will see why in the following program Constraint_Error will be called at run time, before P is even called.

procedure Derived_Types is

  package Pak is
    type Integer_1 is range 1 .. 10;
    procedure P (I: in Integer_1; J: out Integer_1);
    type Integer_2 is new Integer_1'Base range 8 .. 12;
  end Pak;

  package body Pak is
    procedure P (I: in Integer_1; J: out Integer_1) is
    begin
      J := I - 1;
    end P;
  end Pak;

  use Pak;

  B: Integer_2 := 11;  Y: Integer_2;

begin

  P (B, Y);

end Derived_Types;

Subtype categories

Ada supports various categories of subtypes which have different abilities. Here is an overview in alphabetical order.

Anonymous subtype

A subtype which does not have a name assigned to it. Such a subtype is created with a variable declaration:

X : String (1 .. 10) := (others => ' ');

Here, (1 .. 10) is the constraint. This variable declaration is equivalent to:

subtype Anonymous_String_Type is String (1 .. 10);

X : Anonymous_String_Type := (others => ' ');

Base type

In Ada, all types are anonymous and only subtypes may be named. For scalar types, there is a special subtype of the anonymous type, called the base type, which is nameable with the 'Base attribute. The base type comprises all values of the first subtype. Some examples:

 type Int is range 0 .. 100;

The base type Int'Base is a hardware type selected by the compiler that comprises the values of Int. Thus it may have the range -2⁷ .. 2⁷-1 or -2¹⁵ .. 2¹⁵-1 or any other such type.

 type Enum  is (A, B, C, D);
 type Short is new Enum range A .. C;

Enum'Base is the same as Enum, but Short'Base also holds the literal D.

Constrained subtype

A subtype of an indefinite subtype that adds constraints. The following example defines a 10 character string sub-type.

 subtype String_10 is String (1 .. 10);

You cannot partially constrain an unconstrained subtype:

 type My_Array is array (Integer range <>, Integer range <>) of Some_Type;

 -- subtype Constr is My_Array (1 .. 10, Integer range <>);  illegal

 subtype Constr is My_Array (1 .. 10, -100 .. 200);

Constraints for all indices must be given, the result is necessarily a definite subtype.

Definite subtype

A definite subtype is a subtype whose size is known at compile-time. All subtypes which are not indefinite subtypes are, by definition, definite subtypes.

Objects of definite subtypes may be declared without additional constraints.

Indefinite subtype

An indefinite subtype is a subtype whose size is not known at compile-time but is dynamically calculated at run-time. An indefinite subtype does not by itself provide enough information to create an object; an additional constraint or explicit initialization expression is necessary in order to calculate the actual size and therefore create the object.

X : String := "This is a string";

X is an object of the indefinite (sub)type String. Its constraint is derived implicitly from its initial value. X may change its value, but not its bounds.

It should be noted that it is not necessary to initialize the object from a literal. You can also use a function. For example:

X : String := Ada.Command_Line.Argument (1);

This statement reads the first command-line argument and assigns it to X.

A subtype of an indefinite subtype that does not add a constraint only introduces a new name for the original subtype (a kind of renaming under a different notion).

 subtype My_String is String;

My_String and String are interchangeable.

Named subtype

A subtype which has a name assigned to it. “First subtypes” are created with the keyword type (remember that types are always anonymous, the name in a type declaration is the name of the first subtype), others with the keyword subtype. For example:

type Count_To_Ten is range 1 .. 10;

Count_to_Ten is the first subtype of a suitable integer base type. However, if you would like to use this as an index constraint on String, the following declaration is illegal:

subtype Ten_Characters is String (Count_to_Ten);

This is because String has Positive as its index, which is a subtype of Integer (these declarations are taken from package Standard):

subtype Positive is Integer range 1 .. Integer'Last;

type String is (Positive range <>) of Character;

So you have to use the following declarations:

subtype Count_To_Ten is Integer range 1 .. 10;
subtype Ten_Characters is String (Count_to_Ten);

Now Ten_Characters is the name of that subtype of String which is constrained to Count_To_Ten. You see that posing constraints on types versus subtypes has very different effects.

Unconstrained subtype

Any indefinite type is also an unconstrained subtype. However, unconstrainedness and indefiniteness are not the same.

 type My_Enum is (A, B, C);
 type My_Record (Discriminant: My_Enum) is ...;

 My_Object_A: My_Record (A);

This type is unconstrained and indefinite because you need to give an actual discriminant for object declarations; the object is constrained to this discriminant which may not change.

When however a default is provided for the discriminant, the type is definite yet unconstrained; it allows to define both, constrained and unconstrained objects:

 type My_Enum is (A, B, C);
 type My_Record (Discriminant: My_Enum := A) is ...;

 My_Object_U: My_Record;      -- unconstrained object
 My_Object_B: My_Record (B);  -- constrained to discriminant B like above

Here, My_Object_U is unconstrained; upon declaration, it has the discriminant A (the default) which however may change.

Incompatible subtypes

 type My_Integer is range -10 .. + 10;
 subtype My_Positive is My_Integer range + 1 .. + 10;
 subtype My_Negative is My_Integer range -10 .. -  1;

These subtypes are of course incompatible.

Another example are subtypes of a discriminated record:

 type My_Enum is (A, B, C);
 type My_Record (Discriminant: My_Enum) is ...;
 subtype My_A_Record is My_Record (A);
 subtype My_C_Record is My_Record (C);

Also these subtypes are incompatible.

Qualified expressions

In most cases, the compiler is able to infer the type of an expression; for example:

type Enum is (A, B, C);
E : Enum := A;

Here the compiler knows that A is a value of the type Enum. But consider:

procedure Bad is
   type Enum_1 is (A, B, C);
   procedure P (E : in Enum_1) is... -- omitted
   type Enum_2 is (A, X, Y, Z);
   procedure P (E : in Enum_2) is... -- omitted
begin
   P (A); -- illegal: ambiguous
end Bad;

The compiler cannot choose between the two versions of P; both would be equally valid. To remove the ambiguity, you use a qualified expression:

   P (Enum_1'(A)); -- OK

As seen in the following example, this syntax is often used when creating new objects. If you try to compile the example, it will fail with a compilation error since the compiler will determine that 256 is not in range of Byte.

with Ada.Text_IO;

procedure Convert_Evaluate_As is
   type Byte     is mod 2**8;
   type Byte_Ptr is access Byte;

   package T_IO renames Ada.Text_IO;
   package M_IO is new Ada.Text_IO.Modular_IO (Byte);

   A : constant Byte_Ptr := new Byte'(256);
begin
   T_IO.Put ("A = ");
   M_IO.Put (Item  => A.all,
             Width =>  5,
             Base  => 10);
end Convert_Evaluate_As;

You should use qualified expression when getting a string literal's length.

"foo"'Length                  -- compilation error: prefix of attribute must be a name
                              --                    qualify expression to turn it into a name
String'("foo" & "bar")'Length -- 6

Type conversions

Data do not always come in the format you need them. You must, then, face the task of converting them. As a true multi-purpose language with a special emphasis on "mission critical", "system programming" and "safety", Ada has several conversion techniques. The most difficult part is choosing the right one, so the following list is sorted in order of utility. You should try the first one first; the last technique is a last resort, to be used if all others fail. There are also a few related techniques that you might choose instead of actually converting the data.

Since the most important aspect is not the result of a successful conversion, but how the system will react to an invalid conversion, all examples also demonstrate faulty conversions.

Explicit type conversion

An explicit type conversion looks much like a function call; it does not use the tick (apostrophe, ') like the qualified expression does.

Type_Name (Expression)

The compiler first checks that the conversion is legal, and if it is, it inserts a run-time check at the point of the conversion; hence the name checked conversion. If the conversion fails, the program raises Constraint_Error. Most compilers are very smart and optimise away the constraint checks; so, you need not worry about any performance penalty. Some compilers can also warn that a constraint check will always fail (and optimise the check with an unconditional raise).

Explicit type conversions are legal:

• between any two numeric types
• between any two subtypes of the same type
• between any two types derived from the same type (note special rules for tagged types)
• between array types under certain conditions (see RM 4.6(24.2/2..24.7/2))
• and nowhere else

(The rules become more complex with class-wide and anonymous access types.)

I: Integer := Integer (10);  -- Unnecessary explicit type conversion
J: Integer := 10;            -- Implicit conversion from universal integer
K: Integer := Integer'(10);  -- Use the value 10 of type Integer: qualified expression
                             -- (qualification not necessary here).

This example illustrates explicit type conversions:

with Ada.Text_IO;

procedure Convert_Checked is
   type Short is range -128 .. +127;
   type Byte  is mod 256;

   package T_IO renames Ada.Text_IO;
   package I_IO is new Ada.Text_IO.Integer_IO (Short);
   package M_IO is new Ada.Text_IO.Modular_IO (Byte);

   A : Short := -1;
   B : Byte;
begin
   B := Byte (A);  -- range check will lead to Constraint_Error
   T_IO.Put ("A = ");
   I_IO.Put (Item  =>  A,
             Width =>  5,
             Base  => 10);
   T_IO.Put (", B = ");
   M_IO.Put (Item  =>  B,
             Width =>  5,
             Base  => 10);
end Convert_Checked;

Explicit conversions are possible between any two numeric types: integers, fixed-point and floating-point types. If one of the types involved is a fixed-point or floating-point type, the compiler not only checks for the range constraints (thus the code above will raise Constraint_Error), but also performs any loss of precision necessary.

Example 1: the loss of precision causes the procedure to only ever print "0" or "1", since P / 100 is an integer and is always zero or one.

with Ada.Text_IO;
procedure Naive_Explicit_Conversion is
   type Proportion is digits 4 range 0.0 .. 1.0;
   type Percentage is range 0 .. 100;
   function To_Proportion (P : in Percentage) return Proportion is
   begin
      return Proportion (P / 100);
   end To_Proportion;
begin
   Ada.Text_IO.Put_Line (Proportion'Image (To_Proportion (27)));
end Naive_Explicit_Conversion;

Example 2: we use an intermediate floating-point type to guarantee the precision.

with Ada.Text_IO;
procedure Explicit_Conversion is
   type Proportion is digits 4 range 0.0 .. 1.0;
   type Percentage is range 0 .. 100;
   function To_Proportion (P : in Percentage) return Proportion is
      type Prop is digits 4 range 0.0 .. 100.0;
   begin
      return Proportion (Prop (P) / 100.0);
   end To_Proportion;
begin
   Ada.Text_IO.Put_Line (Proportion'Image (To_Proportion (27)));
end Explicit_Conversion;

You might ask why you should convert between two subtypes of the same type. An example will illustrate this.

subtype String_10 is String (1 .. 10);
X: String := "A line long enough to make the example valid";
Slice: constant String := String_10 (X (11 .. 20));

Here, Slice has bounds 1 and 10, whereas X (11 .. 20) has bounds 11 and 20.

type Unpacked is record
  -- any components
end record;

type Packed is new Unpacked;
for  Packed use record
  -- component clauses for some or for all components
end record;

P: Packed;
U: Unpacked;

P := Packed (U);  -- packs U
U := Unpacked (P);  -- unpacks P

package Device_Driver is
   type Size_Type is range 0 .. 64;
   type Register is record
      A, B : Boolean;
      Size : Size_Type;
   end record;

   procedure Read (R : out Register);
   procedure Write (R : in Register);
end Device_Driver;

package body Device_Driver is
   type Hardware_Register is new Register; -- Derived type.
   for Hardware_Register use record
      A at 0 range 0 .. 0;
      B at 0 range 1 .. 1;
      Size at 0 range 2 .. 7;
   end record;

   function Get return Hardware_Register; -- Body omitted
   procedure Put (H : in Hardware_Register); -- Body omitted

   procedure Read (R : out Register) is
      H : Hardware_Register := Get;
   begin
      R := Register (H); -- Explicit conversion.
   end Read;

   procedure Write (R : in Register) is
   begin
      Put (Hardware_Register (R)); -- Explicit conversion.
   end Write;
end Device_Driver;

type Parent_Type is tagged null record;
type Child_Type  is new Parent_Type with null record;

Child_Instance  : Child_Type;

-- View conversion from the child type to the parent type:
Parent_View : Parent_Type := Parent_Type (Child_Instance);

procedure P (Parent_View : Parent_Type'Class) is
   -- View conversion to the child type:
   One : Child_Type := Child_Type (Parent_View);

   -- View conversion to the class-wide child type:
   Two : Child_Type'Class := Child_Type'Class (Parent_View);

type Parent_Type is tagged record
   <components>;
end record;
type Child_Type is new Parent_Type with record
   <further components>;
end record;

Child_Instance : Child_Type;
Parent_View    : Parent_Type'Class renames Parent_Type'Class (Child_Instance);

type My_Array is array (Positive range <>) of Something;
A: My_Array (50 .. 100);

     A'Address = A(A'First)'Address

generic   type Source (<>) is limited private;
   type Target (<>) is limited private;
function Ada.Unchecked_Conversion (S : Source) return Target;

with Ada.Text_IO;
with Ada.Unchecked_Conversion;

procedure Convert_Unchecked is

   type Short is range -128 .. +127;
   type Byte  is mod 256;

   package T_IO renames Ada.Text_IO;
   package I_IO is new Ada.Text_IO.Integer_IO (Short);
   package M_IO is new Ada.Text_IO.Modular_IO (Byte);

   function Convert is new Ada.Unchecked_Conversion (Source => Short,
                                                     Target => Byte);

   A : constant Short := -1;
   B : Byte;

begin

   B := Convert (A);
   T_IO.Put ("A = ");
   I_IO.Put (Item  =>  A,
             Width =>  5,
             Base  => 10);
   T_IO.Put (", B = ");
   M_IO.Put (Item  =>  B,
             Width =>  5,
             Base  => 10);

end Convert_Unchecked;

for Target'Address use expression;
pragma Import (Ada, Target);

with Ada.Text_IO;

procedure Convert_Address_Mapping is
   type Short is range -128 .. +127;
   type Byte  is mod 256;

   package T_IO renames Ada.Text_IO;
   package I_IO is new Ada.Text_IO.Integer_IO (Short);
   package M_IO is new Ada.Text_IO.Modular_IO (Byte);

   A : aliased Short;
   B : aliased Byte;
  
   for B'Address use A'Address;
  pragma Import (Ada, B);
  
begin
   A := -1;
   T_IO.Put ("A = ");
   I_IO.Put (Item  =>  A,
             Width =>  5,
             Base  => 10);
   T_IO.Put (", B = ");
   M_IO.Put (Item  =>  B,
             Width =>  5,
             Base  => 10);
end Convert_Address_Mapping;

type T is range 1 .. 10;

 S1: constant := Integer'Last + Integer'Last;       -- "+" of Integer
 S2: constant := Long_Integer'Last + 1;             -- "+" of Long_Integer
 S3: constant := S1 + S2;                           -- "+" of root_integer
 S4: constant := Integer'Last + Long_Integer'Last;  -- illegal

 S5: constant := Integer'Pos (Integer'Last) + Long_Integer'Pos (Long_Integer'Last);  -- "+" of root_integer

I := 10;
J :=  8;
K := (I + J) - 12;
-- I := I + J;  -- range check would fail, leading to Constraint_Error

 type Color is (Red, Green, Blue);
 type Intensity is range 0 .. 255;
 
 type Colored_Point is array (Color) of Intensity;