Ada Programming/Mathematical calculations
< Ada ProgrammingAda is very well suited for all kind of calculations. You can define you own fixed point and floating point types and — with the aid of generic packages call all the mathematical functions you need. In that respect Ada is on par with Fortran. This module will show you how to use them and while we progress we create a simple RPN calculator.
Simple calculations
Addition
Additions can be done using the predefined operator +. The operator is predefined for all numeric types and the following, working code, demonstrates its use:
-- A.10.1: The Package Text_IO (Annotated) with Ada.Text_IO; procedure Numeric_1 is type Value_Type is digits 12 range -999_999_999_999.0e999 .. 999_999_999_999.0e999; package T_IO renames Ada.Text_IO; package F_IO is new Ada.Text_IO.Float_IO (Value_Type); Value_1 : Value_Type; Value_2 : Value_Type; begin T_IO.Put ("First Value : "); F_IO.Get (Value_1); T_IO.Put ("Second Value : "); F_IO.Get (Value_2); F_IO.Put (Value_1); T_IO.Put (" + "); F_IO.Put (Value_2); T_IO.Put (" = "); F_IO.Put (Value_1 + Value_2); end Numeric_1;
Subtraction
Subtractions can be done using the predefined operator -. The following extended demo shows the use of + and - operator together:
-- A.10.1: The Package Text_IO (Annotated) with Ada.Text_IO; procedure Numeric_2 is type Value_Type is digits 12 range -999_999_999_999.0e999 .. 999_999_999_999.0e999; package T_IO renames Ada.Text_IO; package F_IO is new Ada.Text_IO.Float_IO (Value_Type); Value_1 : Value_Type; Value_2 : Value_Type; Result : Value_Type; Operation : Character; begin T_IO.Put ("First Value : "); F_IO.Get (Value_1); T_IO.Put ("Second Value : "); F_IO.Get (Value_2); T_IO.Put ("Operation : "); T_IO.Get (Operation); case Operation is when '+' => Result := Value_1 + Value_2; when '-' => Result := Value_1 - Value_2; when others => T_IO.Put_Line ("Illegal Operation."); goto Exit_Numeric_2; end case; F_IO.Put (Value_1); T_IO.Put (" "); T_IO.Put (Operation); T_IO.Put (" "); F_IO.Put (Value_2); T_IO.Put (" = "); F_IO.Put (Result); <<Exit_Numeric_2>> return; end Numeric_2;
Purists might be surprised about the use of goto — but some people prefer the use of goto over the use of multiple return statements if inside functions — given that, the opinions on this topic vary strongly. See the isn't goto evil article.
Multiplication
Multiplication can be done using the predefined operator *. For a demo see the next chapter about Division.
Division
Divisions can be done using the predefined operators /, mod, rem. The operator / performs a normal division, mod returns a modulus division and rem returns the remainder of the modulus division.
The following extended demo shows the use of the +, -, * and / operators together as well as the use of a four number wide stack to store intermediate results:
The operators mod and rem are not part of the demonstration as they are only defined for integer types.
with Ada.Text_IO; procedure Numeric_3 is procedure Pop_Value; procedure Push_Value; type Value_Type is digits 12 range -999_999_999_999.0e999 .. 999_999_999_999.0e999; type Value_Array is array (Natural range 1 .. 4) of Value_Type; package T_IO renames Ada.Text_IO; package F_IO is new Ada.Text_IO.Float_IO (Value_Type); Values : Value_Array := (others => 0.0); Operation : String (1 .. 40); Last : Natural; procedure Pop_Value is begin Values (Values'First + 1 .. Values'Last) := Values (Values'First + 2 .. Values'Last) & 0.0; end Pop_Value; procedure Push_Value is begin Values (Values'First + 1 .. Values'Last) := Values (Values'First .. Values'Last - 1); end Push_Value; begin Main_Loop: loop T_IO.Put (">"); T_IO.Get_Line (Operation, Last); if Last = 1 and then Operation (1) = '+' then Values (1) := Values (1) + Values (2); Pop_Value; elsif Last = 1 and then Operation (1) = '-' then Values (1) := Values (1) + Values (2); Pop_Value; elsif Last = 1 and then Operation (1) = '*' then Values (1) := Values (1) * Values (2); Pop_Value; elsif Last = 1 and then Operation (1) = '/' then Values (1) := Values (1) / Values (2); Pop_Value; elsif Last = 4 and then Operation (1 .. 4) = "exit" then exit Main_Loop; else Push_Value; F_IO.Get (From => Operation, Item => Values (1), Last => Last); end if; Display_Loop: for I in reverse Value_Array'Range loop F_IO.Put (Item => Values (I), Fore => F_IO.Default_Fore, Aft => F_IO.Default_Aft, Exp => 4); T_IO.New_Line; end loop Display_Loop; end loop Main_Loop; return; end Numeric_3;
Exponential calculations
All exponential functions are defined inside the generic package Ada.Numerics.Generic_Elementary_Functions.
Power of
Calculation of the form 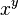 are performed by the operator **. Beware: There are two versions of this operator. The predefined operator ** allows only for Standard.Integer to be used as exponent. If you need to use a floating point type as exponent you need to use the ** defined in Ada.Numerics.Generic_Elementary_Functions.
are performed by the operator **. Beware: There are two versions of this operator. The predefined operator ** allows only for Standard.Integer to be used as exponent. If you need to use a floating point type as exponent you need to use the ** defined in Ada.Numerics.Generic_Elementary_Functions.
Root
The square root 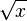 is calculated with the function
is calculated with the function Sqrt(). There is no function defined to calculate an arbitrary root ![\sqrt[n]{x}](../I/m/5e4352778f3b156f05ef056f9793ec36.png) . However you can use logarithms to calculate an arbitrary root using the mathematical identity:
. However you can use logarithms to calculate an arbitrary root using the mathematical identity: ![\sqrt[b]{a} = e^{\log_e (a) / b}](../I/m/b899f3bd66df3cf44eb68dcaab0c9523.png) which will become
which will become root := Exp (Log (a) / b) in Ada. Alternatively, use ![\sqrt[b]{a}=a^{\frac1b}](../I/m/87efd63ce5acdaf8ed14aaac85c0b442.png) which, in Ada, is
which, in Ada, is root := a**(1.0/b).
Logarithm
Ada.Numerics.Generic_Elementary_Functions defines a function for both the arbitrary logarithm 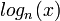 and the natural logarithm
and the natural logarithm 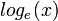 , both of which have the same name
, both of which have the same name Log() distinguished by the number of parameters.
Demonstration
The following extended demo shows the how to use the exponential functions in Ada. The new demo also uses Unbounded_String instead of Strings which make the comparisons easier.
Please note that from now on we won't copy the full sources any more. Do follow the download links to see the full program.
with Ada.Text_IO;
with Ada.Numerics.Generic_Elementary_Functions;
with Ada.Strings.Unbounded;
procedure Numeric_4 is
package Str renames Ada.Strings.Unbounded;
package T_IO renames Ada.Text_IO;
procedure Pop_Value;
procedure Push_Value;
function Get_Line return Str.Unbounded_String;
type Value_Type is digits 12 range
-999_999_999_999.0e999 .. 999_999_999_999.0e999;
type Value_Array is array (Natural range 1 .. 4) of Value_Type;
package F_IO is new Ada.Text_IO.Float_IO (Value_Type);
package Value_Functions is new Ada.Numerics.Generic_Elementary_Functions (
Value_Type);
use Value_Functions;
use type Str.Unbounded_String;
Values : Value_Array := (others => 0.0);
Operation : Str.Unbounded_String;
Dummy : Natural;
function Get_Line return Str.Unbounded_String is
BufferSize : constant := 2000;
Retval : Str.Unbounded_String := Str.Null_Unbounded_String;
Item : String (1 .. BufferSize);
Last : Natural;
begin
Get_Whole_Line :
loop
T_IO.Get_Line (Item => Item, Last => Last);
Str.Append (Source => Retval, New_Item => Item (1 .. Last));
exit Get_Whole_Line when Last < Item'Last;
end loop Get_Whole_Line;
return Retval;
end Get_Line;
...
begin
Main_Loop :
loop
T_IO.Put (">");
Operation := Get_Line;
...
elsif Operation = "e" then
-- insert e
Push_Value;
Values (1) := Ada.Numerics.e;
elsif Operation = "**" or else Operation = "^" then
-- power of x^y
Values (1) := Values (1) ** Values (2);
Pop_Value;
elsif Operation = "sqr" then
-- square root
Values (1) := Sqrt (Values (1));
elsif Operation = "root" then
-- arbritary root
Values (1) :=
Exp (Log (Values (2)) / Values (1));
Pop_Value;
elsif Operation = "ln" then
-- natural logarithm
Values (1) := Log (Values (1));
elsif Operation = "log" then
-- based logarithm
Values (1) :=
Log (Base => Values (1), X => Values (2));
Pop_Value;
elsif Operation = "exit" then
exit Main_Loop;
else
Push_Value;
F_IO.Get
(From => Str.To_String (Operation),
Item => Values (1),
Last => Dummy);
end if;
...
end loop Main_Loop;
return;
end Numeric_4;
Higher math
Trigonometric calculations
The full set of trigonometric functions are defined inside the generic package Ada.Numerics.Generic_Elementary_Functions. All functions are defined for 2π and an arbitrary cycle value (a full cycle of revolution).
Please note the difference of calling the Arctan () function.
with Ada.Text_IO;
with Ada.Numerics.Generic_Elementary_Functions;
with Ada.Strings.Unbounded;
procedure Numeric_5 is
...
procedure Put_Line (Value : in Value_Type);
use Value_Functions;
use type Str.Unbounded_String;
Values : Value_Array := (others => 0.0);
Cycle : Value_Type := Ada.Numerics.Pi;
Operation : Str.Unbounded_String;
Dummy : Natural;
...
procedure Put_Line (Value : in Value_Type) is
begin
if abs Value_Type'Exponent (Value) >=
abs Value_Type'Exponent (10.0 ** F_IO.Default_Aft)
then
F_IO.Put
(Item => Value,
Fore => F_IO.Default_Aft,
Aft => F_IO.Default_Aft,
Exp => 4);
else
F_IO.Put
(Item => Value,
Fore => F_IO.Default_Aft,
Aft => F_IO.Default_Aft,
Exp => 0);
end if;
T_IO.New_Line;
return;
end Put_Line;
...
begin
Main_Loop :
loop
Display_Loop :
for I in reverse Value_Array'Range loop
Put_Line (Values (I));
end loop Display_Loop;
T_IO.Put (">");
Operation := Get_Line;
...
elsif Operation = "deg" then
-- switch to degrees
Cycle := 360.0;
elsif Operation = "rad" then
-- switch to degrees
Cycle := Ada.Numerics.Pi;
elsif Operation = "grad" then
-- switch to degrees
Cycle := 400.0;
elsif Operation = "pi" or else Operation = "π" then
-- switch to degrees
Push_Value;
Values (1) := Ada.Numerics.Pi;
elsif Operation = "sin" then
-- sinus
Values (1) := Sin (X => Values (1), Cycle => Cycle);
elsif Operation = "cos" then
-- cosinus
Values (1) := Cos (X => Values (1), Cycle => Cycle);
elsif Operation = "tan" then
-- tangents
Values (1) := Tan (X => Values (1), Cycle => Cycle);
elsif Operation = "cot" then
-- cotanents
Values (1) := Cot (X => Values (1), Cycle => Cycle);
elsif Operation = "asin" then
-- arc-sinus
Values (1) := Arcsin (X => Values (1), Cycle => Cycle);
elsif Operation = "acos" then
-- arc-cosinus
Values (1) := Arccos (X => Values (1), Cycle => Cycle);
elsif Operation = "atan" then
-- arc-tangents
Values (1) := Arctan (Y => Values (1), Cycle => Cycle);
elsif Operation = "acot" then
-- arc-cotanents
Values (1) := Arccot (X => Values (1), Cycle => Cycle);
...
end loop Main_Loop;
return;
end Numeric_5;
The Demo also contains an improved numeric output which behaves more like a normal calculator.
Hyperbolic calculations
You guessed it: The full set of hyperbolic functions is defined inside the generic package Ada.Numerics.Generic_Elementary_Functions.
with Ada.Text_IO;
with Ada.Numerics.Generic_Elementary_Functions;
with Ada.Strings.Unbounded;
with Ada.Exceptions;
procedure Numeric_6 is
package Str renames Ada.Strings.Unbounded;
package T_IO renames Ada.Text_IO;
package Exept renames Ada.Exceptions;
...
begin
Main_Loop :
loop
Try :
begin
Display_Loop :
...
elsif Operation = "sinh" then
-- sinus hyperbolic
Values (1) := Sinh (Values (1));
elsif Operation = "cosh" then
-- cosinus hyperbolic
Values (1) := Coth (Values (1));
elsif Operation = "tanh" then
-- tangents hyperbolic
Values (1) := Tanh (Values (1));
elsif Operation = "coth" then
-- cotanents hyperbolic
Values (1) := Coth (Values (1));
elsif Operation = "asinh" then
-- arc-sinus hyperbolic
Values (1) := Arcsinh (Values (1));
elsif Operation = "acosh" then
-- arc-cosinus hyperbolic
Values (1) := Arccosh (Values (1));
elsif Operation = "atanh" then
-- arc-tangents hyperbolic
Values (1) := Arctanh (Values (1));
elsif Operation = "acoth" then
-- arc-cotanents hyperbolic
Values (1) := Arccoth (Values (1));
...
exception
when An_Exception : others =>
T_IO.Put_Line
(Exept.Exception_Information (An_Exception));
end Try;
end loop Main_Loop;
return;
end Numeric_6;
As added bonus this version supports error handling and therefore won't just crash when an illegal calculation is performed.
Complex arithmethic
For complex arithmetic Ada provides the package Ada.Numerics.Generic_Complex_Types. This package is part of the "special need Annexes" which means it is optional. The open source Ada compiler GNAT implements all "special need Annexes" and therefore has complex arithmetic available.
Since Ada supports user defined operators, all (+, -, *) operators have their usual meaning as soon as the package Ada.Numerics.Generic_Complex_Types has been instantiated (package ... is new ...) and the type has been made visible (use type ...)
Ada also provides the packages Ada.Text_IO.Complex_IO and Ada.Numerics.Generic_Complex_Elementary_Functions which provide similar functionality to their normal counterparts. But there are some differences:
- Ada.Numerics.Generic_Complex_Elementary_Functions supports only the exponential and trigonometric functions which make sense in complex arithmetic.
- Ada.Text_IO.Complex_IO is a child package of Ada.Text_IO and therefore needs its own with. Note: the
Ada.Text_IO.Complex_IOGet () function is pretty fault tolerant - if you forget the "," or the "()" pair it will still parse the input correctly.
So, with only a very few modifications you can convert your "normals" calculator to a calculator for complex arithmetic:
with Ada.Text_IO.Complex_IO;
with Ada.Numerics.Generic_Complex_Types;
with Ada.Numerics.Generic_Complex_Elementary_Functions;
with Ada.Strings.Unbounded;
with Ada.Exceptions;
procedure Numeric_7 is
...
package Complex_Types is new Ada.Numerics.Generic_Complex_Types (
Value_Type);
package Complex_Functions is new
Ada.Numerics.Generic_Complex_Elementary_Functions (
Complex_Types);
package C_IO is new Ada.Text_IO.Complex_IO (Complex_Types);
type Value_Array is
array (Natural range 1 .. 4) of Complex_Types.Complex;
procedure Put_Line (Value : in Complex_Types.Complex);
use type Complex_Types.Complex;
use type Str.Unbounded_String;
use Complex_Functions;
Values : Value_Array :=
(others => Complex_Types.Complex'(Re => 0.0, Im => 0.0));
...
procedure Put_Line (Value : in Complex_Types.Complex) is
begin
if (abs Value_Type'Exponent (Value.Re) >=
abs Value_Type'Exponent (10.0 ** C_IO.Default_Aft))
or else (abs Value_Type'Exponent (Value.Im) >=
abs Value_Type'Exponent (10.0 ** C_IO.Default_Aft))
then
C_IO.Put
(Item => Value,
Fore => C_IO.Default_Aft,
Aft => C_IO.Default_Aft,
Exp => 4);
else
C_IO.Put
(Item => Value,
Fore => C_IO.Default_Aft,
Aft => C_IO.Default_Aft,
Exp => 0);
end if;
T_IO.New_Line;
return;
end Put_Line;
begin
...
elsif Operation = "e" then
-- insert e
Push_Value;
Values (1) :=
Complex_Types.Complex'(Re => Ada.Numerics.e, Im => 0.0);
...
elsif Operation = "pi" or else Operation = "π" then
-- insert pi
Push_Value;
Values (1) :=
Complex_Types.Complex'(Re => Ada.Numerics.Pi, Im => 0.0);
elsif Operation = "sin" then
-- sinus
Values (1) := Sin (Values (1));
elsif Operation = "cos" then
-- cosinus
Values (1) := Cot (Values (1));
elsif Operation = "tan" then
-- tangents
Values (1) := Tan (Values (1));
elsif Operation = "cot" then
-- cotanents
Values (1) := Cot (Values (1));
elsif Operation = "asin" then
-- arc-sinus
Values (1) := Arcsin (Values (1));
elsif Operation = "acos" then
-- arc-cosinus
Values (1) := Arccos (Values (1));
elsif Operation = "atan" then
-- arc-tangents
Values (1) := Arctan (Values (1));
elsif Operation = "acot" then
-- arc-cotanents
Values (1) := Arccot (Values (1));
...
return;
end Numeric_7;
Vector and Matrix Arithmetic
Ada supports vector and matrix Arithmetic for both normal real types and complex types. For those, the generic packages Ada.Numerics.Generic_Real_Arrays and Ada.Numerics.Generic_Complex_Arrays are used. Both packages offer the usual set of operations, however there is no I/O package and understandably, no package for elementary functions.
Since there is no I/O package for vector and matrix I/O creating a demo is by far more complex — and hence not ready yet. You can have a look at the current progress which will be a universal calculator merging all feature.
Status: Stalled - for a Vector and Matrix stack we need Indefinite_Vectors — which are currently not part of GNAT/Pro. Well I could use the booch components ...
See also
Wikibook
- Ada Programming
- Ada Programming/Delimiters/-
- Ada Programming/Libraries/Ada.Numerics.Generic_Complex_Types
- Ada Programming/Libraries/Ada.Numerics.Generic_Elementary_Functions
Ada 95 Reference Manual
- 4.4: Expressions (Annotated)
- A.5.1: Elementary Functions (Annotated)
- A.10.1: The Package Text_IO (Annotated)
- G.1: Complex Arithmetic (Annotated)
- G.3: Vector and Matrix Manipulation (Annotated)
Ada 2005 Reference Manual