Abstract Algebra/Group Theory/Group/Cancellation
< Abstract Algebra < Group Theory < GroupTheorem
- Let G be a Group.
- 1.
- 2.
Proof
0. Choose such that 1. definition of inverse of g in G (usage 1) 2. 0. 3. is associative in G 4. g-1 is inverse of g (usage 3) 5. eG is identity of G(usage 3)
Diagrams
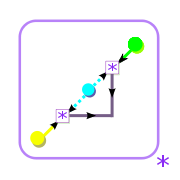 |
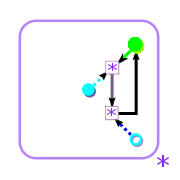 |
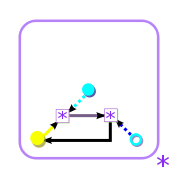 |
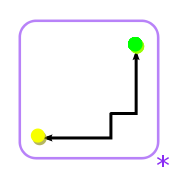 |
Usage
- if a, b, x are in the same group, and x*a = x*b, then a = b
Notice
- a, b, and g have to be all in the same group.
- has to be the binary operator of the group.
- G has to be a group.
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.