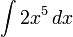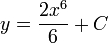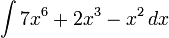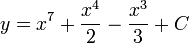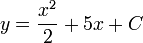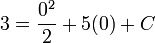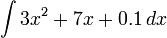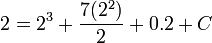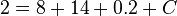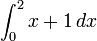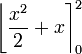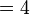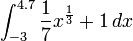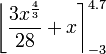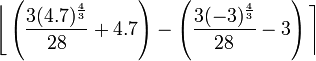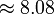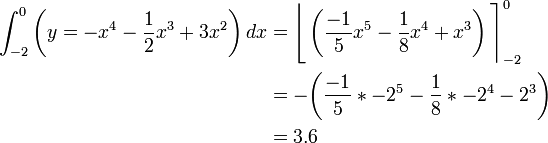A-level Mathematics/OCR/C2/Integration/Solutions

< A-level Mathematics < OCR < C2 < Integration

Worked Solutions

1a)

\int 2x^5 \, dx
Using our rule: That 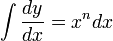\int \frac{dy}{dx} = x^n dx is equal to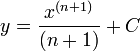 y = \frac {x^{(n + 1)}}{(n + 1)} + C
We get:
y = \frac {2x^6}{6} + C

b)

\int 7x^6 + 2x^3 - x^2 \, dx
Again using our rule, we would get:
y = x^7 + \frac {x^4}{2} - \frac {x^3}{3} + C

2a)

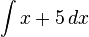\int x +5 \,dx given that the point 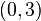(0, 3) lies on the curve.
Using our rule, the intergral becomes
y = \frac {x^2}{2} + 5x + C
Now we can sub in our points 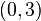(0, 3), So that:
3 = \frac {0^2}{2} + 5(0) + C
Therefore C = 3

b)

\int 3x^2 + 7x +0.1 \,dx
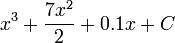
Evaulating this we get: x^3 + \frac {7x^2}{2} + 0.1x + C
Given (2,2), subing these points in:
2 = 2^3 + \frac {7(2^2)}{2} + 0.2 + C
2 = 8 + 14 + 0.2 + C
C = -20.2

3a)

\int_{0}^{2} x + 1 \,dx
Evaluating this we get:
\Bigg\lfloor \frac {x^2}{2} + x \Bigg\rceil_{0}^{2}
Substituting in values we get:
\Bigg\lfloor \left(\frac {2^2}{2} + 2\right) - \left(\frac {0^2}{2} + 0\right) \Bigg\rceil
= 4


b)

\int_{-3}^{4.7} \frac{1}{7}x^{\frac{1}{3}} + 1 \,dx
Evaluating this we get:
\Bigg\lfloor \frac {3x^{\frac{4}{3}}}{28} + x \Bigg\rceil_{-3}^{4.7}


\Bigg\lfloor \left(\frac {3(4.7)^{\frac{4}{3}}}{28} + 4.7\right) - \left(\frac {3(-3)^{\frac{4}{3}}}{28} -3\right) \Bigg\rceil
\approx 8.08


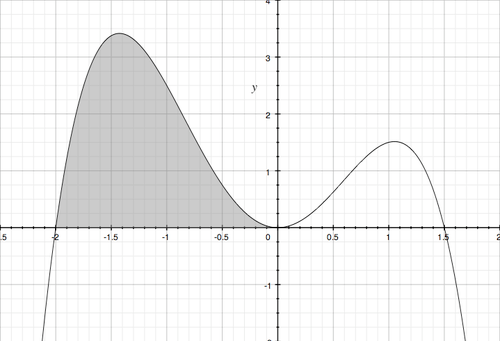
4)

The question is simply to evaluate this definite integral:
\begin{align} \int_{-2}^{0} \bigg(y=-x^4-\frac{1}{2}x^3+3x^2 \bigg) \,dx &= \Bigg\lfloor \left(\frac{-1}{5}x^5-\frac{1}{8}x^4+x^3\right) \Bigg\rceil_{-2}^{0} \\&= -\bigg(\frac{-1}{5}*-2^5-\frac{1}{8}*-2^4-2^3 \bigg) \\&=3.6 \end{align}

5 )

\int tan^4 A
This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.