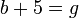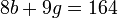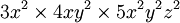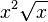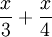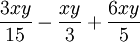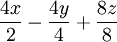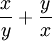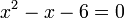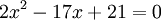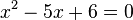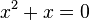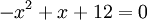A-level Mathematics/OCR/C1/Equations/Problems

< A-level Mathematics < OCR < C1 < Equations

Manipulating Equations

Collecting Like Terms

x + x
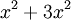
$x^2 + 3x^2$
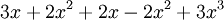
$3x + 2x^2 + 2x -2x^2 + 3x^3$
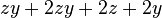
$zy + 2zy + 2z + 2y$
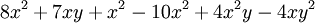
$8x^2 + 7xy + x^2 - 10x^2 + 4x^2y - 4xy^2$

Multiplication

$2x \times 2x$
$6xy \times 3xy$
$6zb \times 3x \times 2ab$
$3x^2 \times 4xy^2 \times 5x^2y^2z^2$
$x^2 \sqrt {x}$

Fractions

$\frac{x}{2} + \frac{x}{2}$
$\frac{x}{3} + \frac{x}{4}$
$\frac{3xy}{15} - \frac{xy}{3} + \frac{6xy}{5}$
$\frac{4x}{2} - \frac{4y}{4} + \frac{8z}{8}$
$\frac{x}{y} + \frac{y}{x}$

Solving Equations

Changing the Subject of an Equation

Solve for x.
$y = 2x$
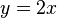
Solve for z.
$x = 3z + 8$
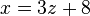
Solve for y.
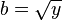
$b = \sqrt{y}$
Solve for x.
$y = x^2 - 9$
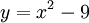
Solve for b.
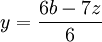
$y = \frac{6b - 7z}{6}$

Solving Quadratic Equations

Find the Roots of:

$x^2 - x -6 = 0$
$2x^2 - 17x + 21 = 0$
$x^2 - 5x + 6 = 0$
$x^2 + x = 0$
$-x^2 + x + 12 = 0$

Simultaneous Equations

Example 1

At a record store, 2 albums and 1 single costs £10. 1 album and 2 singles cost £8. Find the cost of an album and the cost of a single.

Taking an album as 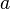$a$ and a single as $s$ , the two equations would be:

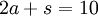
$2a+s=10$

$a+2s=8$

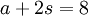
You can now solve the equations and find the individual costs.

Example 2

Tom has a budget of £10 to spend on party food. He can buy 5 packets of crisps and 8 bottles of drink, or he can buy 10 packets of crisps and 6 bottles of drink.

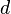Taking a packet of crisps as $c$ and a bottle of drink as $d$ , the two equations would be:

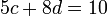
$5c+8d=10$

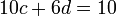
$10c+6d=10$

Now you can solve the equations to find the cost of each item.

Example 3

At a sweetshop, a gobstopper costs 5p more than a gummi bear. 8 gummi bears and nine gobstoppers cost £1.64.

Taking a gobstopper as 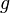$g$ and a gummi bear as 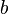$b$ , the two equations would be:

$b+5=g$

$8b+9g=164$

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.