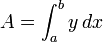A-level Mathematics/AQA/MPC2

< A-level Mathematics < AQA

Sequences and series

Notation

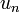$u_n \,\!$ — the general term of a sequence; the n^th term

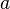$a \,\!$ — the first term of a sequence

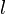$l \,\!$ — the last term of a sequence

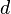$d \,\!$ — the common difference of an arithmetic progression

$r \,\!$ — the common ratio of a geometric progression

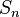$S_n \,\!$ — the sum to n terms: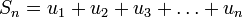 $S_n = u_1 + u_2 + u_3 + \ldots + u_n \,\!$

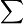$\sum \,\!$ — the sum of

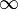$\infty \,\!$ — infinity (which is a concept, not a number)

$n \rightarrow \infty \,\!$ — n tends towards infinity (n gets bigger and bigger)

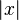$|x| \,\!$ — the modulus of x (the value of x, ignoring any minus signs)

Convergent, divergent and periodic sequences

Convergent sequences

A sequence is convergent if its n^th term gets closer to a finite number, L, as n approaches infinity. L is called the limit of the sequence:

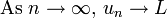
$\mbox{As } n \to \infty \mbox{, } u_n \to L \,\!$

Another way of denoting the same thing is:

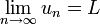
$\lim_{n \to \infty}u_n = L \,\!$

Definition of the limit of a convergent sequence

Generally, the limit 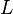$L \,\!$ of a sequence defined by 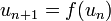$u_{n+1} = f(u_n) \,\!$ is given by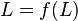 $L = f(L) \,\!$

Divergent sequences

Sequences that do not tend to a limit as 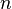$n$ increases are described as divergent. eg: 1, -1 , 1 -1

Periodic sequences

Sequences that move through a regular cycle (oscillate) are described as periodic.

Series

A series is the sum of the terms of a sequence. Those series with a countable number of terms are called finite series and those with an infinite number of terms are called infinite series.

Arithmetic progressions

An arithmetic progression, or AP, is a sequence in which the difference between any two consecutive terms is a constant called the common difference. To get from one term to the next, you simply add the common difference:

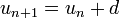
$u_{n+1} = u_n + d \,\!$

Expression for the n^th term of an AP

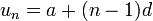
$u_n = a + (n-1)d \,\!$

Formulae for the sum of the first n terms of an AP

The sum of an arithmetic progression is called an arithmetic series.

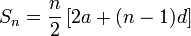
$S_n = \frac{n}{2} \left \lbrack 2a + (n-1)d \right \rbrack \,\!$

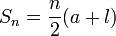
$S_n = \frac{n}{2} (a+l) \,\!$

Formulae for the sum of the first n natural numbers

The natural numbers are the positive integers, i.e. 1, 2, 3…

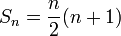
$S_n = \frac{n}{2} (n+1) \,\!$

Geometric progressions

An geometric progression, or GP, is a sequence in which the ratio between any two consecutive terms is a constant called the common ratio. To get from one term to the next, you simply multiply by the common ratio:

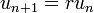
$u_{n+1} = ru_n \,\!$

Expression for the nth term of an GP

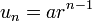
$u_n = ar^{n-1} \,\!$

Formula for the sum of the first n terms of a GP

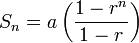
$S_n = a \left ( \frac{1-r^n}{1-r} \right ) \,\!$

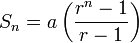
$S_n = a \left ( \frac{r^n-1}{r-1} \right ) \,\!$

Formula for the sum to infinity of a GP

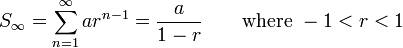
$S_\infty = \sum_{n=1}^\infty ar^{n-1} = \frac{a}{1-r} \qquad \mbox{where } -1 < r < 1 \,\!$

Binomial theorem

The binomial theorem is a formula that provides a quick and effective method for expanding powers of sums, which have the general form 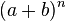$(a+b)^n$ .

Binomial coefficients

The general expression for the coefficient of the 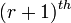$(r+1)^{th}$ term in the expansion of $(1+x)^n$ is:

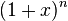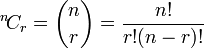
${}^n\!C_r = \binom{n}{r} = \frac{n!}{r!(n-r)!}$

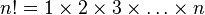
where $n! = 1 \times 2 \times 3 \times \ldots \times n$

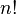$n!$ is called n factorial. By definition, $0!=1$ .

Binomial expansion of (1+x)ⁿ

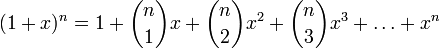
$(1+x)^n=1+\binom{n}{1}x+\binom{n}{2}x^2+\binom{n}{3}x^3+\ldots+x^n$

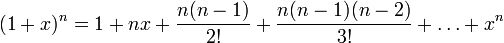
$(1+x)^n=1+nx+\frac{n(n-1)}{2!}+\frac{n(n-1)(n-2)}{3!}+\ldots+x^n$

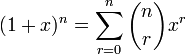
$(1+x)^n=\sum_{r=0}^n\binom{n}{r}x^r$

Trigonometry

Arc length

$l = r \theta \,\!$

Sector area

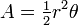
$A = \tfrac{1}{2} r^2 \theta$

Trigonometric identities

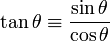
$\tan{\theta} \equiv \frac{\sin{\theta}}{\cos{\theta}}$

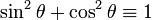
$\sin^2{\theta} + \cos^2{\theta} \equiv 1 \,\!$

Indices and logarithms

Laws of indices

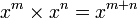
$x^m \times x^n = x^{m+n} \,\!$

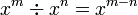
$x^m \div x^n = x^{m-n} \,\!$

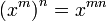
$\left ( x^m \right )^n = x^{mn} \,\!$

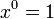$x^0 = 1 \,\!$ (for x ≠ 0)

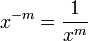
$x^{-m} = \frac{1}{x^m} \,\!$

$x^{\frac{1}{n}} = \sqrt[n]{x} \,\!$

$x^{\frac{m}{n}} = \sqrt[n]{x^m} \,\!$

Logarithms

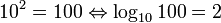
$10^2 = 100 \Leftrightarrow \log_{10}{100} = 2$

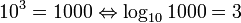
$10^3 = 1000 \Leftrightarrow \log_{10}{1000} = 3$

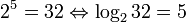
$2^5 = 32 \Leftrightarrow \log_{2}{32} = 5$

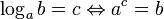
$\log_a{b} = c \Leftrightarrow a^c = b$

Laws of logarithms

The sum of the logs is the log of the product.

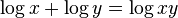
$\log{x} + \log{y} = \log{xy} \,\!$

The difference of the logs is the log of the quotient.

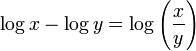
$\log{x} - \log{y} = \log{\left ( \frac{x}{y} \right )}$

The index comes out of the log of the power.

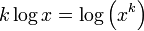
$k\log{x} = \log{\left ( x^k \right )}$

Differentiation

Differentiating the sum or difference of two functions

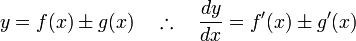
$y = f(x) \pm g(x) \quad \therefore \quad \frac{dy}{dx} = f'(x) \pm g'(x)$

Integration

Integrating axⁿ

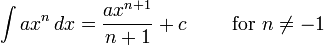
$\int ax^n \, dx = \frac{ ax^{n+1} }{ n+1 } + c \qquad \mbox{ for } n \neq -1 \,\!$

Area under a curve

The area under the curve 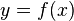$y = f(x)$ between the limits $x = a$ and $x = b$ is given by

$A = \int_a^b y \, dx$

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.