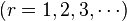A-level Mathematics/AQA/MFP3

< A-level Mathematics < AQA

Series and limits

Two important limits:

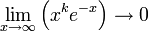$\lim_{x\rightarrow \infty} \left ( x^k e^{-x} \right ) \rightarrow 0$ for any real number k

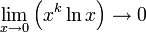$\lim_{x\rightarrow 0} \left ( x^k \ln{x} \right ) \rightarrow 0$ for all k > 0

The basic series expansions

 $( r= 0,1,2,\cdots)$

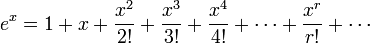
$e ^x = 1+ x + {x^2 \over 2!} + {x^3 \over 3!} + {x^4 \over 4!} + \cdots +{x^r \over r!} + \cdots$

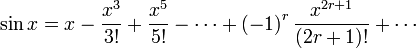
$\sin x = x - {x^3 \over 3!} + {x^5 \over 5!} - \cdots + \left (-1 \right )^r {x^{2r+1} \over (2r+1)!} + \cdots$

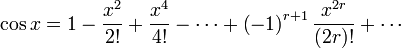
$\cos x = 1 - {x^2 \over 2!} + {x^4 \over 4!} - \cdots + \left (-1 \right )^{r+1} {x^{2r} \over (2r)!} + \cdots$

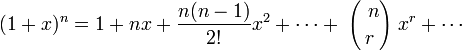
$(1 + x)^n = 1 + nx + {n(n - 1) \over 2!} x^2 + \cdots + \; {\ n \choose r} \; x^r + \cdots$

 $(r= 1,2,3, \cdots)$

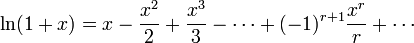
$\ln (1 + x) = x - {x^2 \over 2} + {x^3 \over 3} - \cdots + (-1)^{r+1} {x^r \over r} + \cdots$

Improper intergrals

The integral :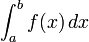 $\int_a^b f(x)\,dx\,$ is said to be improper if

the interval of integration is infinite, or;
f(x) is not defined at one or both of the end points x=a and x=b, or;
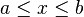f(x) is not defined at one or more interior points of the interval $a \le x \le b$ .

Polar coordinates

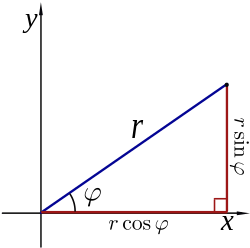
A diagram illustrating the relationship between polar and Cartesian coordinates.

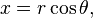
$x = r \cos \theta,\,$

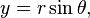
$y = r \sin \theta,\,$

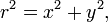
$r^2 = x^2 + y^2,\,$

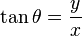
$\tan \theta = {y \over x}$

The area bounded by a polar curve

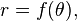
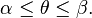
For the curve $r = f(\theta),\,$ $\alpha \le \theta \le \beta.\,$

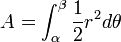
$A = \int_\alpha^\beta {1 \over 2} r^2 d\theta\,$

r must be defined and be non-negative throughout the interval 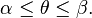$\alpha \le \theta \le \beta. \,$

Numerical methods for the solution of first order differential equations

Euler's formula

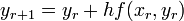
$y_{r + 1} = y_r + hf( x_r, y_r )\,$

The mid-point formula

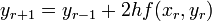
$y_{r + 1} = y_{r - 1} + 2 h f( x_r , y_r )\,$

The improved Eular formula

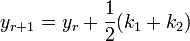
$y_{r + 1} = y_r + {1 \over 2} ( k_1 + k_2 )\,$

where

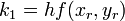
$k_1 = h f ( x_r , y_r)\,$

and

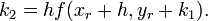
$k_2 = h f ( x_r + h , y_r + k_1 ).\,$

Second order differential equations

Euler's identity

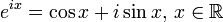
$e^{ix} = \cos x + i \sin x,\, x \in \Bbb {R}\,$

When $x = \pi,\,$ substituting into the identity gives

  $e^{i\pi}=-1\,$

Further reading

The AQA's free textbook

This article is issued from Wikibooks. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.