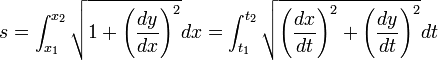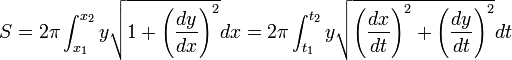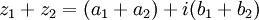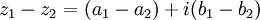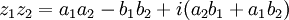A-level Mathematics/AQA/MFP2
< A-level Mathematics < AQARoots of polynomials
The relations between the roots and the coefficients of a polynomial equation; the occurrence of the non-real roots in conjugate pairs when the coefficents of the polynomials are real.
Complex numbers
Square root of minus one
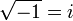

Square root of any negative real number
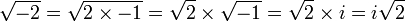

General form of a complex number
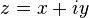
where 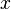 and
and 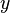 are real numbers
are real numbers
Modulus of a complex number
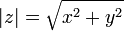
Argument of a complex number
The argument of 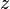 is the angle between the positive x-axis and a line drawn between the origin and the point in the complex plane (see )
is the angle between the positive x-axis and a line drawn between the origin and the point in the complex plane (see )
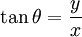
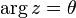
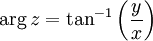
Polar form of a complex number
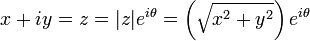
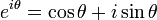
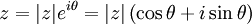
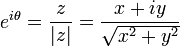
Addition, subtraction and multiplication of complex numbers of the form x + iy
In general, if 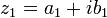 and
and 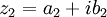 ,
,
Complex conjugates
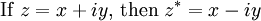
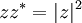
Division of complex numbers of the form x + iy
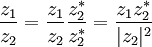
Products and quotients of complex numbers in their polar form
If 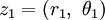 and
and 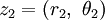 then
then 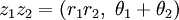 , with the proviso that
, with the proviso that  may have to be added to, or subtracted from,
may have to be added to, or subtracted from,  if
if  is outside the permitted range for
is outside the permitted range for 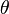 .
.
If 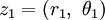 and
and 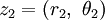 then
then 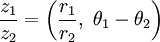 , with the same proviso regarding the size of the angle
, with the same proviso regarding the size of the angle 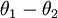 .
.
Equating real and imaginary parts
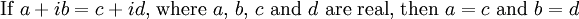
Coordinate geometry on Argand diagrams
If the complex number 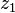 is represented by the point
is represented by the point 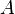 , and the complex number
, and the complex number 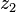 is represented by the point
is represented by the point 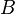 in an Argand diagram, then
in an Argand diagram, then 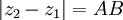 , and
, and 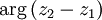 is the angle between
is the angle between 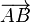 and the positive direction of the x-axis.
and the positive direction of the x-axis.
Loci on Argand diagrams
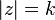 represents a circle with centre
represents a circle with centre  and radius
and radius 
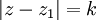 represents a circle with centre
represents a circle with centre 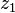 and radius
and radius 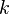
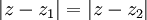 represents a straight line — the perpendicular bisector of the line joining the points
represents a straight line — the perpendicular bisector of the line joining the points 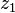 and
and 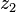
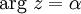 represents the half line through
represents the half line through 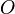 inclined at an angle
inclined at an angle 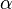 to the positive direction of
to the positive direction of 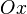
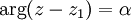 represents the half line through the point
represents the half line through the point 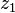 inclined at an angle
inclined at an angle 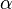 to the positive direction of
to the positive direction of 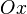
De Moivre's theorem and its applications
De Moivre's theorem
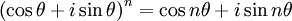
De Moivre's theorem for integral n
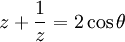
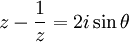
Exponential form of a complex number
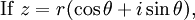
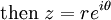
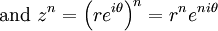
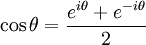
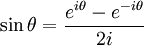
The cube roots of unity
The cube roots of unity are  ,
, 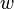 and
and 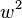 , where
, where
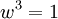
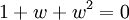
and the non-real roots are
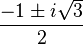
The nth roots of unity
The equation  has roots
has roots
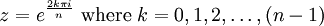
The roots of zn = α where α is a non-real number
The equation 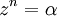 , where
, where 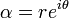 , has roots
, has roots
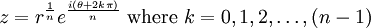
Hyperbolic functions
Definitions of hyperbolic functions
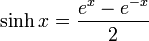
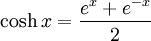
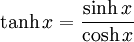
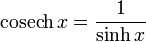
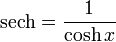
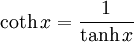
Hyperbolic identities
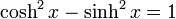
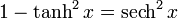
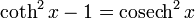
Addition formulae
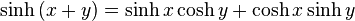
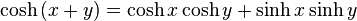
Double angle formulae
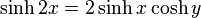
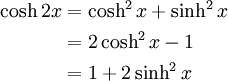
Osborne's rule
Osborne's rule states that:
- to change a trigonometric function into its corresponding hyperbolic function, where a product of two sines appears, change the sign of the corresponding hyperbolic form
Note that Osborne's rule is an aide mémoire, not a proof.
Differentiation of hyperbolic functions
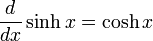
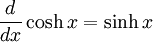
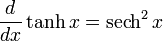
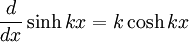
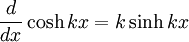
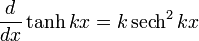
Integration of hyperbolic functions
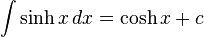
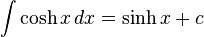
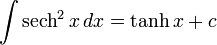
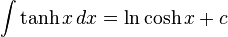
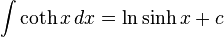
Inverse hyperbolic functions
Logarithmic form of inverse hyperbolic functions
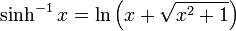
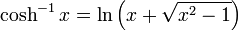
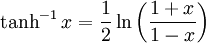
Derivatives of inverse hyperbolic functions
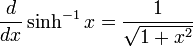
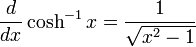
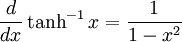
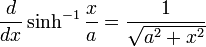
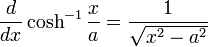
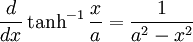
Integrals which integrate to inverse hyperbolic functions
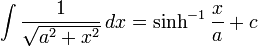
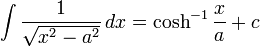
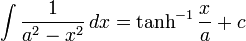
Arc length and area of surface of revolution
Calculation of the arc length of a curve and the area of a surface using Cartesian or parametric coordinates